Container with most water

Question

Given n non-negative integers a1, a2, ..., an, where each represents a point at a coordinate (i, ai). n vertical lines are drawn such that the two endpoints of the line i are at (i, ai) and (i, 0). Find two lines, which, together with the x-axis form a container, such that the container contains the most water.

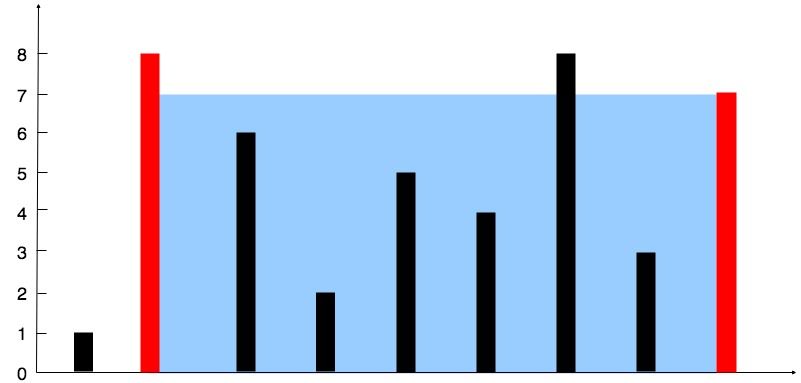
Input: height = [1,8,6,2,5,4,8,3,7]

Output: 49

Explanation: The above vertical lines are represented by an array [1,8,6,2,5,4,8,3,7]. In this case, the maximum area of water (blue section) the container can contain is 49.

Now, let's see how can we solve this problem.

Solution

Brute Force Approach

Here, we will try all the combinations starting from the first index to the last one.

So we will try combinations like : (1, 1), (1, 2).. (1, n) to (n, 1).. (n, n)

and we will keep a value to check the maximum area we are getting each time. By the end of the iteration, we will get the max area which will be the answer.

Time complexity : O(n ^ 2)

Code:

Here, a JAVA implementation by the Brute Force approach.

public int maxAreaBruteForce(int[] height) {
        int maxArea = 0;
        for (int i = 0; i < height.length; i++) {
            for (int j = i + 1; j < height.length; j++) {
                int temp = Math.min(height[i], height[j]) * (j - i);
                maxArea = Math.max(maxArea, temp);
            }
        }
        return maxArea;
    }

Now let us check if we can bring down the time complexity to Linear time

Enhanced solution

We will try to find an intuition over here:

The max area for any rectangle would be one where width is max. So, considering that both ends have max height, the highest area we will get is considering the first and last values.

Therefore, we will initiate two pointers, left and right like below:

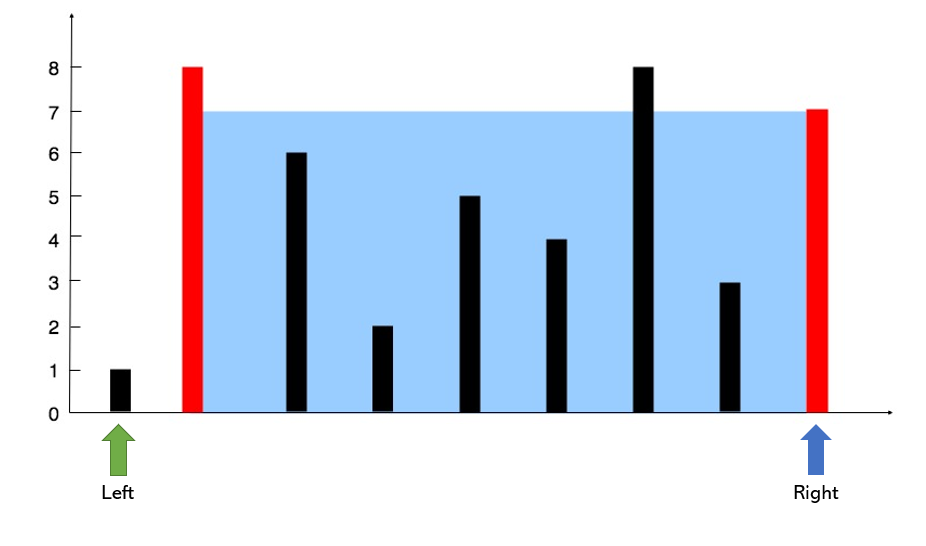
Now, we will calculate the area as length X width. Here length is the height between two i.e., 1 and width is the distance between two pointers i.e., 8. So the total area is 8.

Next, we will see among the two heights, left and right, which is lower.

We will then update the pointer for the pointer whose value is lower.

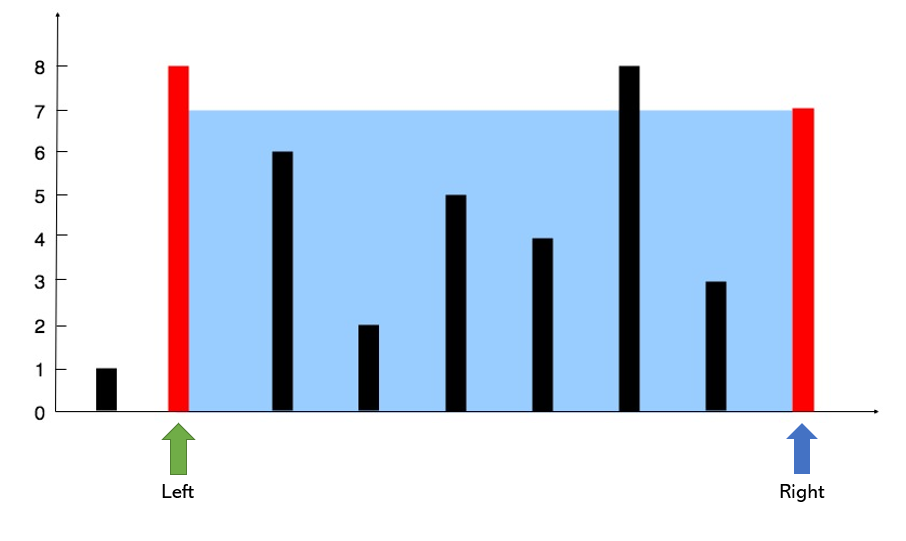
Here, the left has a lower value, so we will update the left as left + 1 and keep the right as it is.

Here again, we will calculate the area. This time L = 7 and width = 7. Hence the area is 7X7 = 49

Comparing this to the previous value of 8, since 49 is higher we will consider this as the answer.

Now among the two pointers, here right has a lower value so, we will update the right pointer as below:

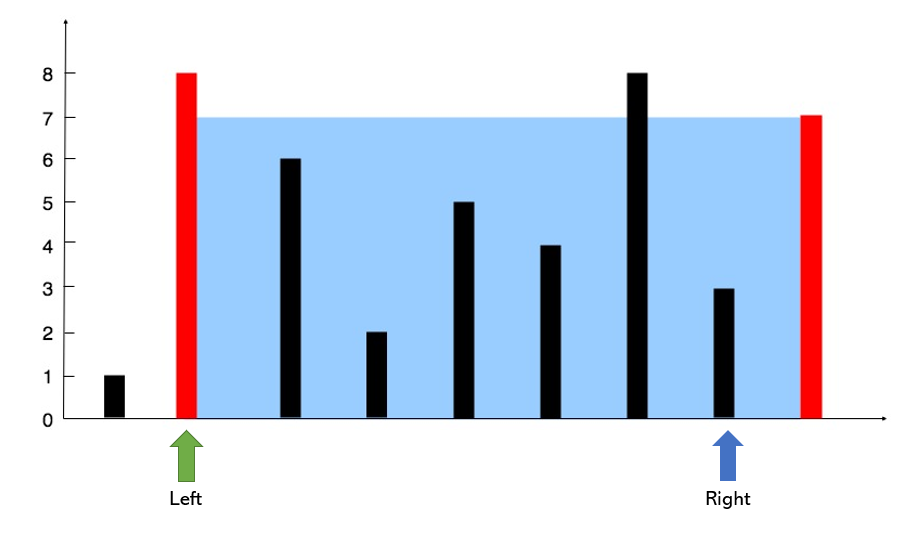
Here, area = 3 X 6 = 18 which is lower than the max we got till now. Hence we will ignore and move forward as below:

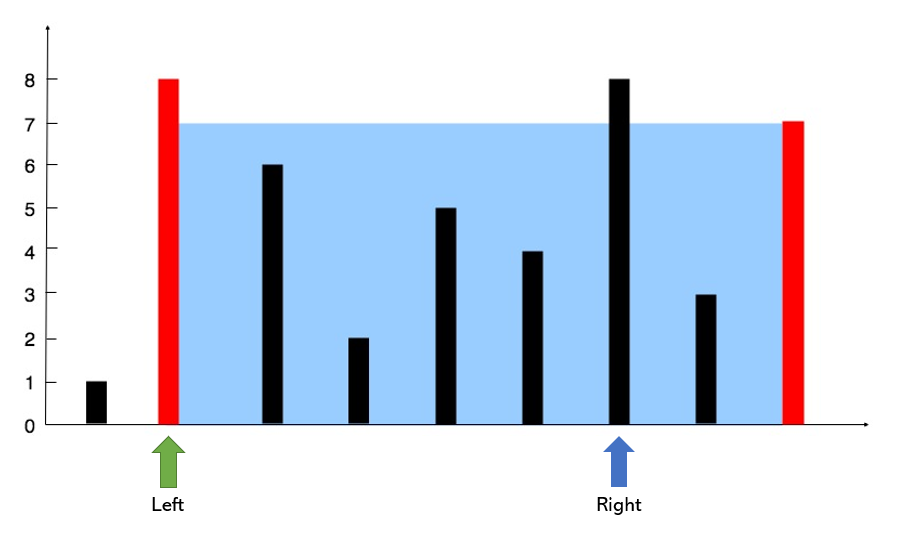
We will carry on this process, calculating the area each time and updating the pointers till the left is less than the right pointer.

As soon as left > right, we will break (Similar to Binary Search 🔍)

At the end, we will be able to find the max area which will be 49 in this case.

Let's see the JAVA implementation:

public int maxArea(int[] height) {
        int left = 0;
        int right = height.length - 1;
        int maxArea = 0;

        while (left < right) {
            maxArea = Math.max(maxArea, Math.min(height[left], height[right]) * (right - left));
            if (height[left] < height[right]) {
                left = left + 1;
            } else {
                right = right - 1;
            }
        }
        return maxArea;
    }

Thus we were able to enhance the solution to a time complexity of O(n) which is way better than the Brute force.

Hope you like it ! I would love to know if you have any other better approach in mind.